FEM-Simulation der Linearmotoren; Entwicklung eines Modells; Nutzen des Modells und Resultate
Sinn einer FEM-Analyse bei der Entwicklung von DLM
Gerade bei vorliegender Anwendung wird von einem Linearmotor aufgrund beschränkter Baumaße bei den geforderten Kraften eine maximale Materialausnutzung benötigt. Ausgehend von der allgemeinen Bemessungsgleichung für elektrische Maschinen ist ersichtlich, daß die Anforderungen an den DLM die bisher gesetzten physikalischen Grenzen sprengt.
Vorausgesetzt, es kann ein funktionierendes FEM-Modell gefunden werden, können damit Motorparameter optimiert bzw. maximiert werden.
Um aus der Physik des Motors das Maximum herauszuholen, gibt es theoretisch drei Möglichkeiten :
Entwurf eines Auslegungsalgorithmus, welcher die FEM schon bei der Projektierung mit einbezieht. Ein derartiger Algorithmus existiert meines Wissens noch nicht.
Manuelle Optimierung; Ein Optimierungsschritt beinhaltet : Entwurf eines Motors mit herkömmlichen Methoden, Bau des Motors, Messungen am Prüfstand, Umarbeiten des Motorsà Bau eines neuen Motors, Messungen am Prüfstandà Definition, wie sich die Parameteränderung auf die Motordaten auswirkt usw. Die Kosten liegen pro Schritt zwischen 5 und 25 TEUR, je nachdem, was am Motor geändert werden muß.
Auslegung des Motors mit herkömmlichen Methoden und Optimierung mit FEM am Rechner. Hierbei liegen die Kosten pro Schritt zwischen 50 und 500 EUR, je nach Art des zu ändernden Parameters.
Anforderungen an ein Modell von DLM zur Simulation mit FEM
Ein Modell muß sämtlichen bekannten physikalischen Eigenschaften des natürlichen Vorbildes genügen. Deshalb sind die bisher verwendeten Modelle für die Simulation von DLM ungeeignet.
Begründung:
Die Erregung wurde mit einem Drehstromsystem vorgenommen
![]()
Nur die angelegte Klemmenspannung ist konstant (vorausgesetzt, der Innenwiderstand des Netzes ist vernachlässigbar gering bzw. das Netz hat eine beliebig große Leistung).
Der Strom durch die Wicklungen stellt sich ein; abhängig von den Parametern des Ersatzschaltbildes (Widerstände des Primärteils, Widerstände des Sekundärteils, Material, Luftspalt usw., Schlupf). Der Strom muß also Resultat der Simulation sein, nicht Ursache!
Folgende Resultate der Simulation müssen dem realen Verhalten des Motors entsprechen :
1. Synchrongeschwindigkeit
Ohne Gegenkraft (FL=0) muß bei Synchrongeschwindigkeit vS=2*f*t die tangentiale Kraft FT=0 sein, d.h., der Motor muss ohne Belastung bis auf Synchrongeschwindigkeit hochlaufen.
2. Arbeitspunkte
Bei verschiedenen Gegenkraften (FL=var.) muss sich im eingeschwungenen Zustand (Dv=0) die Kraft FT=FL einstellen. Die Punkte müssen einer üblichen Geschwindigkeits-Kraft-Kennlinie entsprechen.
3. Generatorbetrieb
Bei einer positiven Gegenkraft FL>0 muß sich die Geschwindigkeit und der Strom erhöhen (oder die Phase ändern); d.h. bei einer Simulation mit einer Anfangsgeschwindgkeit v>vS muß ein deutliches Abbremsen der Geschwindigkeit bis unter vS zu erkennen sein (in Abhängigkeit von v,i,F).
4. Bremsen
Bei einer Gegenkraft größer als die vom Motor erzeugte (|FL|>FT) muß sich bei hohem Strom die Drehrichtung umkehren.
5. Reversieren
Bei Vertauschen zweier Motorphasen muß sich die Drehrichtung ändern.
6. Stromänderung
Es muß eine deutliche Abhängigkeit des Stromes und der sich einstellenden Geschwindigkeit (bei FL=konst.) vom Luftspalt, Material des Sekundärteiles und vom Schlupf erkennbar sein (FT=FT(d,MAT,s) und i=i(d,MAT,s)). Der Strom bei s=0 sollte dem Magnetisierungsstrom entsprechen.
Fazit :
Das Modell muss der Kennlinie, dem Ersatzschaltbild und der Bewegungsgleichung entsprechen !
Grenzen des Modells
Beim Programmpaket Maxwell 2D handelt es sich um ein zweidimensionales Programm. Aufgrund der unvollständigen Modellnachbildung und fehlender Angaben wird dieses Paket niemals die tatsächlichen Sachverhalte im Motor simulieren können. Besonders bezieht sich das auf folgende Punkte :
1. Querrandeffekt
Aufgrund der zweidimensionalen Arbeitsweise kann der Querrandeffekt nicht berücksichtigt werden. Um diesen zu umgehen, wird im allgemeinen die Sekundärteilbreite um ca. 20% breiter als die aktive Eisenfläche ausgeführt, um die elektromagnetische Wellen in diesen Bereichen nicht einzuschnüren.
Maxwell arbeitet scheibchenweise; die Tiefe des Modells (Breite des DLM) wird über einen Faktor definiert. Dabei wird davon ausgegangen, daß alle Teile des Motors die gleiche Breite haben.
2. Längsrandeffekt
Gemäß Ansoft-Ausführung wird der Längsrandeffekt bei deren Modellvorschlägen nicht berücksichtigt (s. Seminarunterlagen Ansoft).
Meines Erachtens wird dieser Effekt (welcher sich besonders beim Einlaufen des Sekundärteiles in den Bereich eines Stators bemerkbar macht) bei unserem Modell jedoch beachtet, was durch Simulation nachgewiesen werden kann.
3. Ummagnetisierungs-/Eisenverluste
Die materialspezifischen Ummagnetisierungs- und Eisenverluste können im Modell nicht definiert werden, so daß eine Berücksichtigung dieser nicht erfolgen kann.
Die Berücksichtigung der Eisenschichtung durch Setzen der Konduktivität des Blechpaketes auf s= 0 S/m ist aus meiner Sicht sehr grob.
4. Streuverluste; Streuinduktivitat
Diese werden nur durch die Angabe der Streuinduktivitat berucksichtigt. Gerade diese zahlenma?ig mit guter Genauigkeit zu erfassen, bereitet Schwierigkeiten. Deshalb wurde hier mit Schätzwerten gearbeitet ( s. Menüpunkt Winding Setup).
5. Erwärmung
Die Widerstandsänderung durch die Erwärmung der Kupferwicklung (Ohmscher Widerstand) kann wie folgt definiert werden :
![]()
Wie sowohl die Messungen als auch die Simulation zeigen, werden hier beachtliche Verlustleistungen im Sekundärteil freigesetzt, die Temperaturanstiege erfolgen damit, zumindest im Inneren der Wicklung, ebenfalls im Millisekundenbereich.
Es muß davon ausgegangen werden, daß die Wicklung nie überall eine konstante Temperatur hat. Dies ist ein zusätzliche Fehlerursache bei der Simulation.
Überlegung :
Gemessen wurde am kalten Motor der Widerstand einer Phase von
RKALT=2,3697 Ohm
Bei Erwärmung des Motors auf 80°C verändert sich der Widerstand wie folgt :
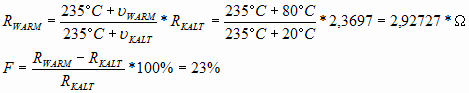
Bei einer Erwärmung des Motors auf 180°C gilt :
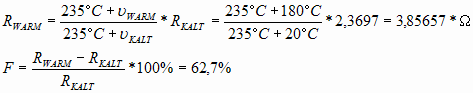
Der Einfluß der Erwärmung wird im Kapitel Parameterempfindlichkeit untersucht.
6. Nutharmonische
Durch die zweidimensionale Arbeitsweise können die Nutschrägungen nicht berücksichtigt werden.
Problematisch ist das beim vorhandenen Krauss-Maffei-Motor, nicht jedoch beim Antrima-Motor, da hier von einem homogenem Sekundärteil ausgegangen wird.
7. Umrichterbetrieb
Bisher wurde die Erregung durch sinusförmige Spannungen angenommen. Wie sich die Daten des Motors ändern bei Erregung durch eine dreiphasige PWM-modulierte Spannung, ist noch nicht untersucht worden.
Ziele der Simulation
Folgende Zielstellungen müssen an die Entwicklung der DLM gestellt werden :
FT=FT(PARM)--> max.
PV=PV(PARM)--> min. (PARM=Luftspalt, Wicklung, Polteilung, Blechgeometrie,Material)
dFT/dt--> 0 (im statischen Betrieb)
Es muß ein Motor entwickelt werden, der die maximale Vorschubkraft bei minimaler Verlustleistung bringt; bei welchem die Kraftriffel jedoch minimal sind.
Das Modell
Der Eröffnungsbildschirm
Abb.1: Eröffnungsbildschirm
Modellzeichnung
Im Punkt Define Modell wird die Zeichnung des Modells erstellt. Hier werden mechanische Abmessungen festgelegt. Da das Original-CAD-Modul recht umständlich ist, wird die Zeichnung aus einer AutoCad-Datei importiert.

Abb.2: Modellzeichnung
Gruppieren von Objekten
Eine Gruppierung der verschiedenen Objekte (z.B. Zusammenfassung einzelner Nuten zu Pasen) wurde hier im Unterschied zum Ansoft-Modellvorschlag nicht durchgeführt, da eine Erregung mit Spannung stattfinden muß. Bei dieser Erregungsmethode ist die Richtung jeder Spulenseite zu definieren..
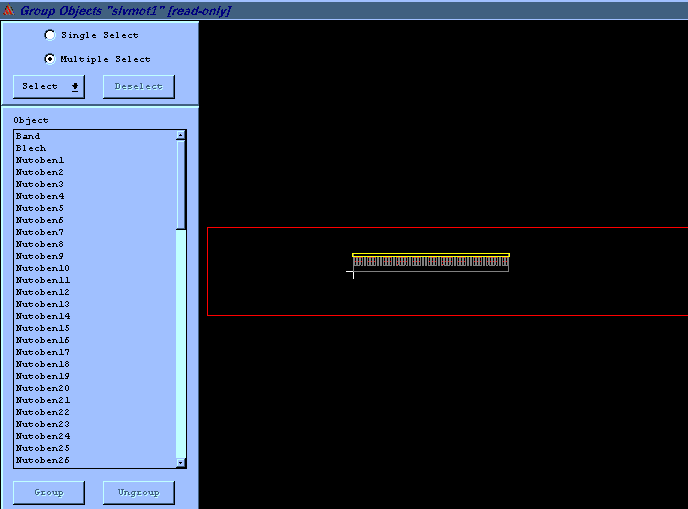
Abb.3: Gruppierung
Materialdefinitionen

Abb. 4: Materialdefinition
In diesem Menupunkt werden allen Objekten Materialeigenschaften zugeordnet. Problematisch ist es hier aus meiner Sicht, dem Elektroblech die Konduktivitat von s=0 S/m zuzuordnen, um die Blechschichtung zu berücksichtigen. Erfahrungen und Messungen haben gezeigt, daß im Blechpaket immer Ströme fließen, trotz Oxidschichten zwischen den einzelnen Blechen. Die elektrische Leitfähigkeit erklärt sich durch Grate im Bereich der Schnittkanten der Bleche beim Zusammenfügen. Ein aus meiner Sicht großer Nachteil des 2-D-Modells.
Die Kennlinie des Elektrobleches wurde wie folgt eingefügt :
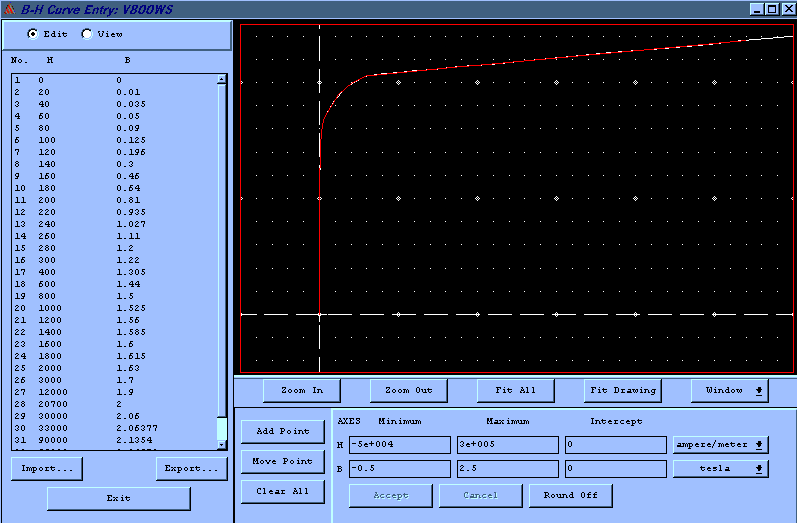
Abb.5: BH-Kennlinie des Elektrobleches
Quellendefinition

Abb.6: Quellendefinition
Anhand dieser Definitionen ist zu sehen, daß als Quelle eine Spannung angenommen wurde; genau so muß es auch sein; der Strom ist dann das Resultat der Simulation
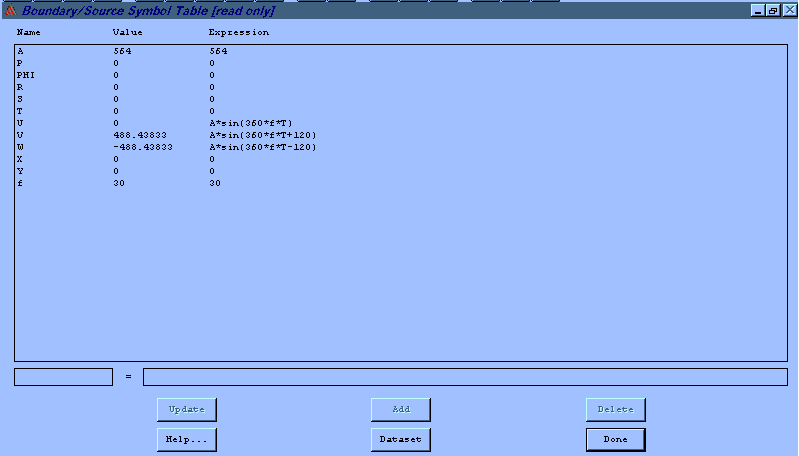
Abb.7: Definition der Spannungen
A bezeichnet die Amplitude des Wechselspannung; bei einer Effektivspannung von 400 V ist das :
![]()
Unklarheiten gibt es bei der Angabe der Wicklungsdaten:
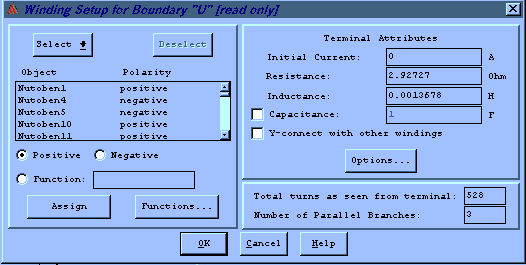
Abb.8: Definition der Phase U
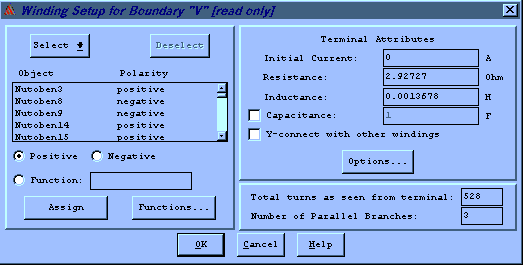
Abb.9: Definition der Phase V

Abb.10: Definition der Phase W
Der ohmsche Widerstand wurde im kalten Zustand am KM-Motor gemessen, dann auf den Widerstand im warmen Zustand umgerechnet. Da es beachtliche Energieeinträge gibt, ist aber der Wicklungswiderstand nie konstant. Wie im Punkt Grenzen des Modells/ 5. Erwärmung gezeigt, kann es hier zu Unterschieden bis zu 63% kommen (s. Parameterempfindlichkeit des Modells)
Ein weiterer Unsicherheitsfaktor ist die Angabe der Streuinduktivität. In der Maxwell-Beschreibung ist nicht definiert, welche Streuinduktivität zur Anwendung kommt. Aufgrund der Wirkungsweise der FEM-Software wurde hier nur die Wickelkopfstreuinduktiviät angegeben (also die, die Maxwell aufgrund der zweidimensionalen Arbeitsweise nicht berechnen kann). Für die numerische Berechnung der Streuinduktivitäten (Erstellung des Systemmodells zur Regelung) sei empfohlen: I.P. Kopylow; Projektirovanie elektriceskih mashin; Moskwa; 1980
Im Kapitel Parameterempfindlichkeit wird jedoch gezeigt, dass sich dieser Parameter nur gering (im Gegensatz zum Ohmschen Widerstand) auf die Vorschubkraft auswirkt.
Solvereinstellungen
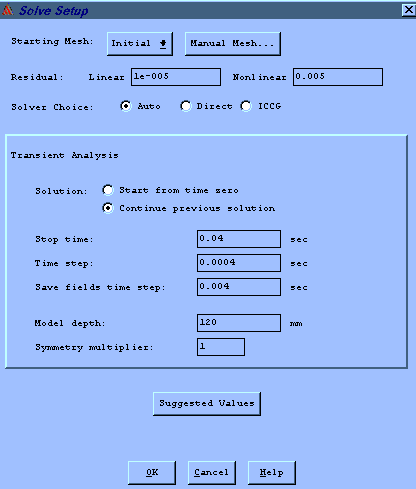
Abb.10: Solvereinstellungen
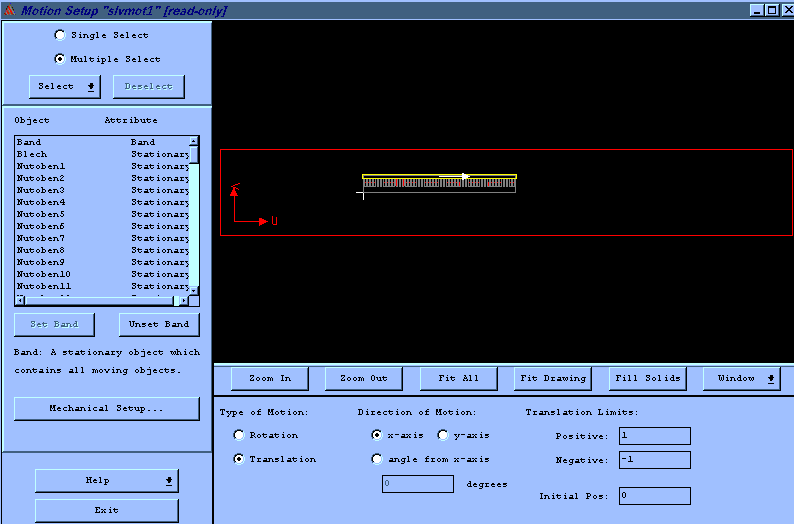
Abb.12: Definition der Sekund
ärteilbewegungNach vielen Stunden Rechenzeit und mehreren Systemabstürzen werden dann die Resultate ausgegeben.
Resultate
Wie die Resultate zu bewerten sind
Für die Bewertung der Resultate sind folgende Regeln wichtig :
Meßdaten bei Versuchen geben als Resultat Effektivwerte; bei Maxwell werden nur Amplitudenwerte ausgegeben. Bei den Angaben in der Tabelle (Resultate) handelt es sich jeweils um Amplitudenwerte (bzw. die Maximalwerte der ersten 40 ms).
Es wurde aus Zeitgründen jeweils nur der Bereich der ersten 40 ms nach dem Zuschalten der Spannung simuliert; ein Effektivwert kann sich, zumindest bei den Kräften noch nicht eingestellt haben.
der Kraftriffel dFT1 ist die absolute Differenz zwischen dem ersten Maximalwert der Vorschubkraft und dem darauf folgendem Minimum
Krauss-Maffei-Motor
Der Motor 3drahws2
Dies ist der Kraus-Maffei-Motor; Das Sekundärteil besteht aus einer 10 mm dicken Kupferplatte mit aufgebrachter 5 mm dicken Platte aus ST37. Der Luftspalt beträgt 0,4 mm, die Überdeckung 500 mm.
Die Amplitude der Klemmenspannung beträgt 328,8 V; die Frequenz 29,2 Hz.
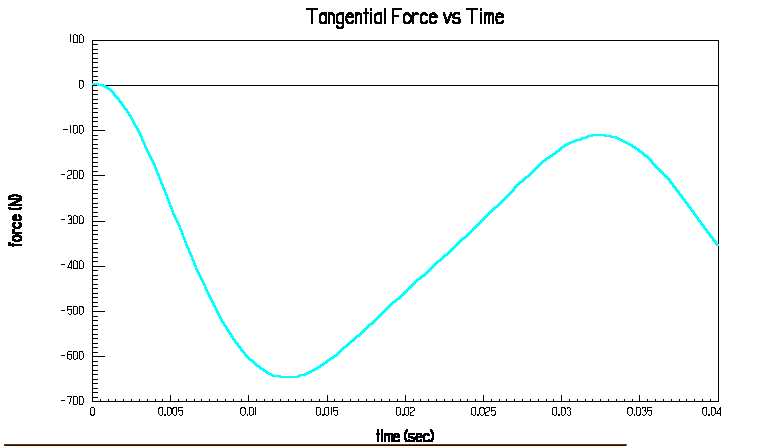
Abb.13: Vorschubkraft des Kraus-Maffei-Motors mit Kupferplatte bei Teillast

Abb.14: Anziehungsktaft des Kraus-Maffei-Motors mit Kupferplatte bei Teillast

Abb.15: Str
öme des Kraus-Maffei-Motors mit Kupferplatte bei Teillast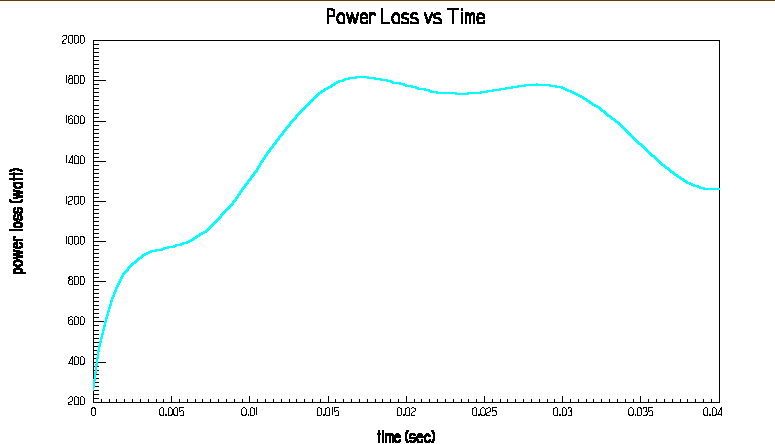
Abb.16: Verlustleistung des Kraus-Maffei-Motors mit Kupferplatte bei Teillast
Unklar ist, welche Verlustleistung errechnet wurde : die des gesamten Systems, die des Primärteiles oder die des Sekundärteiles.
Der Motor 3drahws3
Dieser Motor hat die gleichen Daten wie Motor 3drahws2; einziger Unterschied ist, daß das Sekundärteil aus Aluminium besteht. Auch hier wieder die aufgebrachte ST37-Platte.
Der Motor 3drahws4
Dieser Motor ist der gleiche wie 3drahws3; die Erregung ist jedoch mit einer Wechselspannung von 400 V (Amplitude 564 V) bei 50 Hz vorgenommen worden.
Vergleich der KM-Motoren
|
Motor |
3drahws2 |
3drahws3 |
3drahws4 |
|
Eingabedaten |
|||
|
Stator |
1 |
1 |
1 |
|
Sekundarteil |
Kupfer |
Alu |
Alu |
|
Joch |
ST37 |
ST37 |
ST37 |
|
Luftspalt d, [mm] |
0,4 |
0,4 |
0,4 |
|
UAMPL, [V] |
328,8 |
328,8 |
564 |
|
f, [Hz] |
29,2 |
29,2 |
50 |
|
R, [Ohm] |
2,92727 |
2,92727 |
2,92727 |
|
L, [H] |
0,0013678 |
0,0013678 |
0,0013678 |
|
w, [] |
528 |
528 |
528 |
|
q, [] |
3 |
3 |
3 |
|
Resultate |
|||
|
FT, [N] |
-645,48 |
-755,38 |
-2170,6 |
|
FN, [N] |
1368,61 |
1276,61 |
2872,40 |
|
IAMPL, [A] |
103,69 |
102,58 |
178,39 |
|
PV, [W] |
1816,58 |
2497,27 |
7165,07 |
|
dFT1, [N] |
534,96 |
463,21 |
1209,65 |
Tab.1: Vergleich der Kraus-Maffei-Motoren
Interessant, daß Aluminium als Sekundärteil die höhere Vorschubkraft erzeugt; die Verlustleistung ist hier jedoch höher.
Parameterempfindlichkeit des Modells am Beispiel der Krauss-Maffei-Motoren; Motor 3drahws6 bis 3drahws9
Um zu überprüfen, mit welchen Unsicherheiten bei ungenauen Angaben von Ohmschen Wicklungswiderstand und Streuinduktivität gerechnet werden kann, wurden hierzu Simulationen angestellt. Widerstandswerte wurden aus Grenzen des Modells/5. Erwärmung verwendet; die Streuinduktivität wurde um den Faktor 10 zur ursprünglichen vermindert.
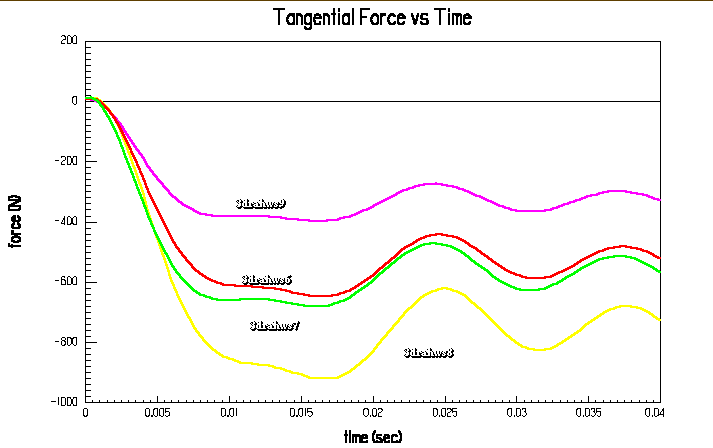
Abb.17: Parameterempfindlichkeit des FEM-Modells
|
Motor |
3drahws6 |
3drahws7 |
3drahws8 |
3drahws9 |
Messung MP15/1 |
|
Eingabedaten |
|||||
|
Stator |
1 |
1 |
1 |
1 |
1 |
|
Sekundärteil 10 mm |
Al |
Al |
Al |
Al |
Al |
|
Joch |
- |
- |
- |
- |
- |
|
Luftspalt d, [mm] |
0,593 |
0,593 |
0,593 |
0,593 |
0,6 |
|
UAMPL, [V] |
442,03 |
442,03 |
442,03 |
442,03 |
442,03 |
|
f, [Hz] |
39,3 |
39,3 |
39,3 |
39,3 |
39,3 |
|
R, [Ohm] |
2,9727 |
2,9727 |
2,3697 |
3,85657 |
2,3697 |
|
L, [H] |
0,0013678 |
0,00013678 |
0,0013678 |
0,0013678 |
- |
|
w, [] |
528 |
528 |
528 |
528 |
528 |
|
q, [] |
3 |
3 |
3 |
3 |
3 |
|
Resultate |
|||||
|
FT, [N] |
-647,13 |
-681,20 |
-920,35 |
-396,35 |
850 |
|
FN, [N] |
1875,14 |
1970,27 |
2437,78 |
1278,61 |
- |
|
IAMPL, [A] |
133,97 |
138,20 |
159,24 |
105,54 |
95,03 |
|
PV, [W] |
3860,99 |
4088,95 |
5464,74 |
2378,76 |
- |
|
dFT1, [N] |
205,5 |
210,13 |
298,8 |
122,5 |
- |
Tab.2: Parameterempfindlichkeit des Modells gegen R, X
sSchlussfolgerungen :
Eine Anderung der Streuinduktivitat zieht nur geringfugige Anderungen der Vorschubkraft nach sich
Die Abhangigkeit vom ohmschen Wicklungswiderstand (und damit von der Wicklungstemperatur) ist beachtlich! Ein Motor, welcher im kalten Zustand (20°C) noch eine Vorschubkraft von FT= 920 N bringt, erreicht im heißen Zustand (180°C; d.h. Widerstandsänderung um 63%) nur noch 397 N (Kraft 56% der ursprünglichen). Da der DLM eigentlich nur im thermisch-transienten Bereich durch den sehr hohen Eintrag von Verlustleistung (Verlustleistung ist direkt proportional dem Schlupf; dieser ist bei unserer Anwendung s=1) arbeitet, wird nie eine zeitlich konstante Kraft erzeugt werden können, es sei denn, daß
a. eine sehr leistungsstarke Kühlung verwendet wird und
b. dem Umrichter ein Kraftregler übergeordnet wird ( wobei wir wieder beim Prinzip der feldorientierten Regelung wären)
Die errechneten Werte liegen im Bereich der gemessenen (s. Meßprotokoll15 Tabelle1; Punkt 313,5V (*Wurzel(2)=442,03V)/39,3 Hz)
Antrima-Motor
Der Motor ANTRIMAMOT
Dieser Motor besitzt 48 Nuten. Im Randpolbereich sind Teile der Zweischichtwicklung in der unteren Nuthälfte untergebracht. Dies, da die Randpole wenig Kraft bringen, diese Art der Anordnung aber Platz spart. Eine maßstäbliche Verringerung der Abmaße des Original-Krauss-Maffei-Motors war aus magnetischer Sicht nicht möglich.
Die Bleche sind gelocht; zum einen mit den Öffnungen für die Bolzen zum Zusammenziehen des Blechpaketes, zum anderen mit den Kühlöffnungen.
Erregt wurde mit einem dreiphasigem Spannungssystem :
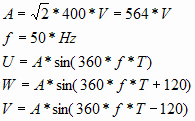
Die Durchführungen für die Kühlrohre wurden in Kupfer ausgeführt und geerdet (U=0); das Sekundärteil besteht aus St37.
Die Definitionen gehen von einer konstanten Vorschubgeschwindigkeit von v=0mm/s aus; die mechanischen transienten Vorgänge(s. Anforderungen an ein FEM-Modell) werden hier außer Acht gelassen, da diese auch beim vorhandenem DLM eine untergeordnete Rolle spielen.
Der Motor ANTRIMAMOT1
Dieser Motor entspricht dem Motor ANTRIMA, jedoch mit folgenden Änderungen :
Das Sekundärteil ist aus Aluminium
Die Kühl- und Befestigungsdurchführungen entfallen
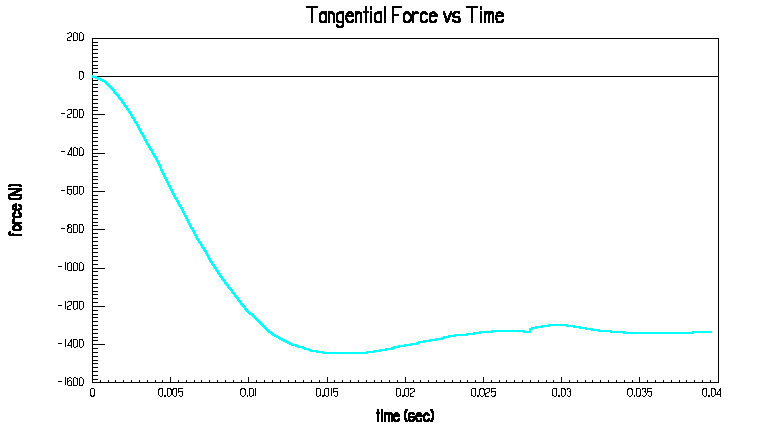
Abb.18: Motor ANTRIMAMOT1; FTMAX=1500N
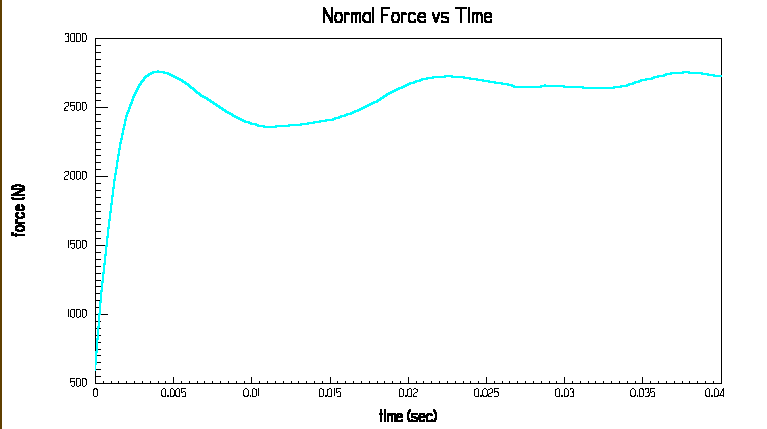
Abb.19: Anziehungskraft des Motors ANTRIMAMOT1; FMAX=2.800 N
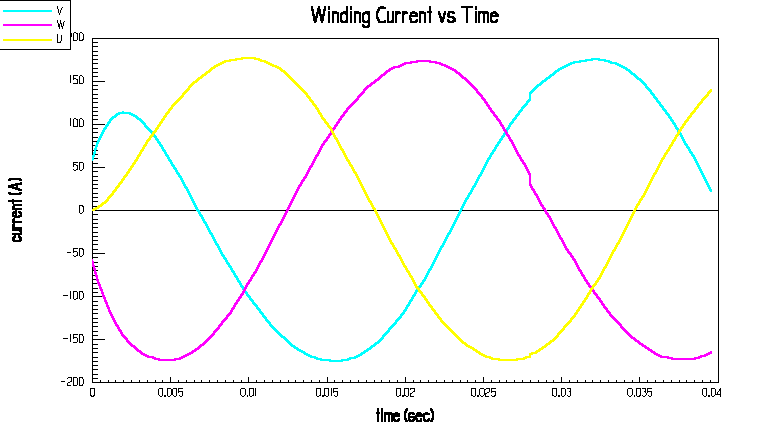
Abb.20: Str
öme des Motors ANTRIMAMOT1; deutlich sind die undefinierbaren Systemabstürze zu erkennen
Der Motor ANTRIMAMOT2
Dieser Motor entspricht dem Motor ANTRIMA1, jedoch mit folgenden Änderungen :
Das Sekundärteil ist aus Kupfer

Abb.21: Vorschubkraft des Motors ANTRIMAMOT2

Abb.22: Anziehungskraft des Motors ANTRIMAMOT2

Abb.23: Str
öme des Motors ANTRIMAMOT2Die Motoren ANTRIMAMOT3 bis ANTRIMAMOT5
Genaueres zu den Daten aller ANTRIMAMOT-Motoren in Tabelle 3.
Vergleich der ANTRIMAMOT-Motoren
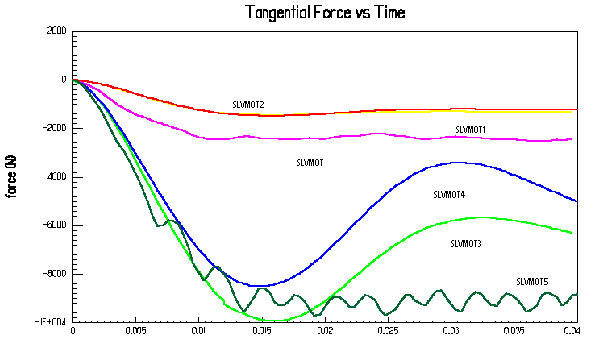
Abb.24: Vergleich der Vorschubkrafte der ANTRIMA-Motoren
|
Motor |
ANTMOT |
ANTMOT1 |
ANTAMOT2 |
ANTMOT3 |
ANTMOT4 |
ANTMOT5 |
|
Eingabedaten |
||||||
|
Stator |
1 |
1 |
1 |
2 |
2 |
2 |
|
Sekundarteil 10 mm |
ST37 |
Al |
Cu |
Al |
Cu |
St37 |
|
Joch |
- |
- |
- |
- |
- |
- |
|
Luftspalt d, [mm] |
0,4 |
0,4 |
0,4 |
2*0,4 |
2*0,4 |
2*0,4 |
|
UAMPL, [V] |
564 |
564 |
564 |
564 |
564 |
564 |
|
f, [Hz] |
30 |
30 |
30 |
30 |
30 |
30 |
|
R, [Ohm] |
2,92727 |
2,92727 |
2,92727 |
2,92727 |
2,92727 |
2,92727 |
|
L, [H] |
0,0013678 |
0,0013678 |
0,0013678 |
0,0013678 |
0,0013678 |
0,0013678 |
|
w, [] |
528 |
528 |
528 |
528 |
528 |
528 |
|
q, [] |
3 |
3 |
3 |
3 |
3 |
3 |
|
Resultate |
||||||
|
FT, [N] |
-2536,05 |
-1488,66 |
-1480,29 |
-9936,3 |
-8495,90 |
-9562,89 |
|
FN, [N] |
-17161,8 |
+2531,32 |
+2759,57 |
57,29 |
58,35 |
-982,02 |
|
IAMPL, [A] |
161,73 |
176,41 |
177,27 |
166,55 |
170,19 |
151,2 |
|
PV, [W] |
13123,3 |
5669,9 |
5632,41 |
32095,60 |
25106,7 |
41437,3 |
|
dFT1, [N] |
144,68 |
188,89 |
272,61 |
4252,83 |
5085,66 |
983,66 |
Tab.3: Vergleich der ANTRIMA-Motoren
Einfluß der Überdeckung
Ausgehend vom Motor ANTRIMAMOT4 wurden mehrere Simulationen mit geringerer Überdeckung durchgeführt. Die Resultate sind folgende :
|
Motor |
ANTMOT4 |
ANTMOT6 |
ANTMOT7 |
ANTMOT8 |
|
Eingabedaten |
||||
|
Stator |
2 |
2 |
2 |
2 |
|
Sekundärteil 10 mm |
Cu |
Cu |
Cu |
Cu |
|
Joch |
- |
- |
- |
- |
|
Luftspalt d, [mm] |
2*0,4 |
2*0,4 |
2*0,4 |
2*0,4 |
|
Uberdeckung, [mm] |
500,00 |
427,17 |
402,90 |
359,14 |
|
Uberdeckung, [%] |
100,0 |
85,4 |
80,6 |
71,8 |
|
UAMPL, [V] |
564 |
564 |
564 |
564 |
|
f, [Hz] |
30 |
30 |
30 |
30 |
|
R, [Ohm] |
2,92727 |
2,92727 |
2,92727 |
2,92727 |
|
L, [H] |
0,0013678 |
0,0013678 |
0,0013678 |
0,0013678 |
|
w, [] |
528 |
528 |
528 |
528 |
|
q, [] |
3 |
3 |
3 |
3 |
|
Resultate |
||||
|
FT, [N] |
-8495,90 |
-7856,31 |
-6531,13 |
-6702,08 |
|
FN, [N] |
58,35 |
23,10 |
23,21 |
20,24 |
|
IAMPL, [A] |
170,19 |
165,82 |
170,53 |
166,68 |
|
PV, [W] |
25106,7 |
24366,1 |
20530,3 |
20148,5 |
|
dFT1, [N] |
5085,66 |
4641,31 |
4689,72 |
3987,12 |
Tab.4: Einfluß der Überdeckung
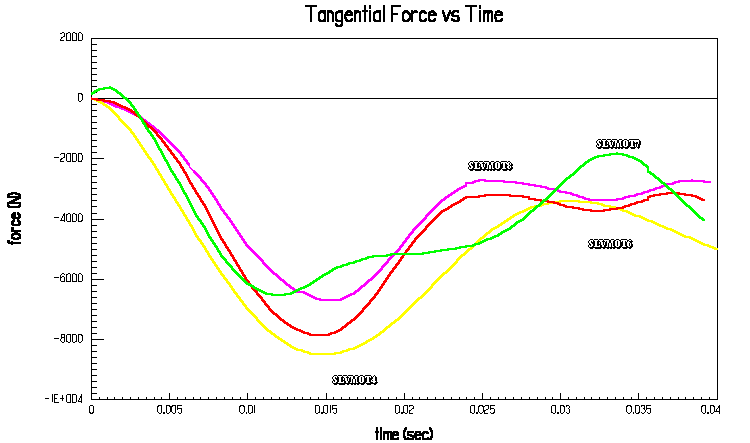
Abb.25: Einfluß der Überdeckung
Aus dem Verlauf der Vorschubkraft bei ANTRIMAMOT7 ist ersichtlich, daß die Höhe und die Form der Kraft nicht nur von der prozentualen Überdeckung abhängig ist, sondern auch noch von den absoluten Koordinaten (Anfangsbedingungen).
Probleme
Die errechneten und gemessenen Motordaten stimmen nicht 100%-ig überein; auf die möglichen Ursachen wurde in Grenzen des Modells hingewiesen
Es treten sehr hohe Verlustleistungen auf.
Obwohl ein reines Eisensekundärteil theoretisch eine kleinere Vorschubkraft zuläßt, sind die Kraftriffel hierbei am kleinsten
Eine Kühlung des Sekundärteiles mit eingefügten Kupferstäben erweist sich als problematisch; sind die Kupferstäbe zu nahe an den Zahnfüßen, fließen sehr hohe Ströme; sind diese weiter weg, so läßt die Kühlleistung nach. Hier sind noch Versuche anzustellen, z.B. mit Kühlregistern aus Miramid.
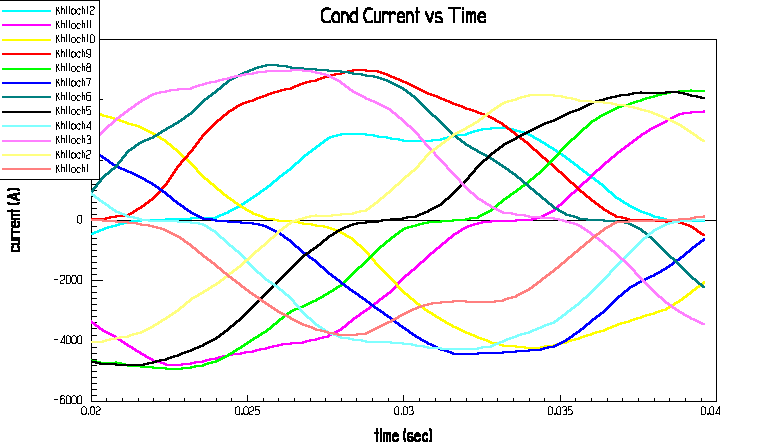
Abb.26: Str
öme in kupfernen Kühlstäben, wenn diese geerdet sind
Fazit
Aufgrund des Vergleiches zwischen gemessenen und simulierten Werten, aber auch der Überlegungen zu den Grenzen des Modells kann folgende Aussage getroffen werden :
Die Simulation eines Linearmotors mit einem 2D-FEM-Modell liefert brauchbare qualitative Aussagen, jedoch unbrauchbare quantitative Aussagen. Grund hierfür ist, daß die Resultate sehr stark vom ohmschen Widerstand der Wicklung und damit von der Temperatur abhängen, ein Zustand des thermischen Gleichgewichts beim vorliegenden Anwendungsfall nicht erreicht werden kann.
Es kann der Einfluß verschiedener Parameter auf das Verhalten des Motors untersucht werden; vielleicht können somit auch prozentuale Änderungen gefunden werden (ändert sich der Luftspalt um das x-fache, verringert sich die Kraft um das y-fache). Es können jedoch nicht die Motordaten berechnet werden.
P. Weiss
![]()
Kontakt: mailto:weiss@patriceweiss.com
Stand: 17.06.2005